LA ELIPSE
La elipse el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.

ELEMENTOS DE LA ELIPSE
RELACIÓN ENTRE LA DISTANCIA FOCAL Y LOS SEMIEJES
Como vemos, hay un momento de la elipse en que se forma un triángulo rectángulo. Por tal razón, usamos el teorema de Pitágoras:
EXCENTRICIDAD DE LA ELIPSE
La excentricidad de una elipse (e) es un valor que determina la forma de la elipse, en el sentido de si es más redondeada o si se aproxima a un segmento. Sea c la semidistancia focal y a el semieje mayor:
La excentricidad puede tomar valores entre 0 y 1 (0≤e≤1). Cuanto más se aproxime a 0, tomará más forma de circunferencia, y cuanto más se aproxime a 1 tomará una forma más achatada.
CASOS DE LA ELIPSE (CON CENTRO DENTRO/FUERA DEL ORIGEN)
La elipse puede darse de distintas formas:
HORIZONTAL

En este caso los focos se ubican en el eje de las x.
Si el centro de la elipse está en el origen se procede con la siguiente fórmula:
Pero, si de lo contrario, el centro está en un punto cualquiera, su fórmula fórmula y ecuación canónica será:VERTICAL

Los focos se ubican en el eje de las y.
Si en centro está en origen, su fórmula es:
Si el centro de está en un punto cualquiera, su fórmula y ecuación canónica es:
INCLINADA
Este es otro caso de la elipse que muy poco se estudia.
Cabe anotar que a siempre será mayor que b (a>b). A partir de esto podemos deducir si la elipse es horizontal o vertical. Si el valor mayor está debajo de X en la fórmula, la elipse es horizantal. Si el valor mayor está debajo de de Y en la fórmula, la elipse es vertical.
ECUACIÓN ORDINARIA
A partir de la ecuación canónica podemos llegar a la ecuación ordinaria haciendo el respectivo proceso matemático. Veamos el siguiente ejemplo:
ECUACIÓN GENERAL
Ahora, a partir de la ecuación ordinaria, podemos obtener la ecuación general de la elipse. Vemos el ejemplo:





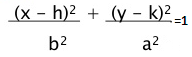




...viaje interestelar aceleración constante (órbitas elípticas)... e, excentricidad >0 y <1 su grado de alargamiento; e=cos B/cos a... elípse, si se define como curva cerrada de la intersección de un plano que corta a una superficie cónica sin pasar por su vértice; a, ángulo de la superficie cónica entre su eje y generatriz; B, ángulo >a y <90º entre el plano y el eje de la superficie cónica.
ResponderEliminar...frenando asteroides, el método más expeditivo: colocar "las nucleares" muy cerca de la superficie... "Boom!", en el Espacio, al no haber aire no hay onda expansiva, lo único que le llega es la radiación que volatiliza el material del punto de impacto y produciendo un chorro a reacción que cambia su órbita... (pag. 135-138. Libro "El Asteroide del Fin del Mundo")
ResponderEliminar...viaje interestelar aceleración constante (motor lineal electromagnético)... ya hay pilas que producen electricidad desde la desintegración radiactiva natural (50 años duran para telf. Móvil). ¿También para un posible Motor de aceleración constante?: un Motor Eléctrico Lineal, Bobinas Electromagnéticas en línea que impulsarían a gran velocidad hacia la→ Popa de la Nave (o más allá de la Popa según donde esté instalado) unas pesadas Bolas de Acero dentro de un Tubo en *U* (la parte abierta hacia la Proa) alineado con el centro de gravedad de la Nave: 1º ◄Impulso por el retroceso→. 2º Impulso, al volver a inercia la Bolas por el otro ramal de la *U* al final impactan hacia la ◄Proa← y "caen", por un Tubo que cierra circuíto en la parte abierta, de nuevo al Inicio de la *U*... (Cañón electromagnético. Libro "El Asteroide del Fin del Mundo" pag. 139).
ResponderEliminar(2)...viaje interestelar aceleración constante (el motor)... Impulso a reacción con recuperación. Nada se pierde... a Popa de la Nave la "tobera" un rectángulo estrecho en forma de *Doble U* de Tubo al Vacío "x" diámetro. Alineado con el eje longitudinal de la Nave el Ramal Recto de Impulsión: un *Tubo* rodeado de Bobinas Electromagnéticas, un Cañón Electromagnético de alimentación continua que impulsa a gran velocidad a un Collar de pesadas Bolas de Acero Sueltas que van por Vía MAGLEV en el lateral exterior del *Tubo*, cada Bola del Collar, Separada de las demás, luego sigue a inercia por el otro Ramal de simple retorno de las *U* para entrar de nuevo al Cañón indefinidamente: ◄Impulso a reacción con recuperación. Nada se pierde, "solo" hace falta mucha energía eléctrica en la Nave: un generador nuclear. Motor de Aceleración Constante.
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarEl cohete eléctrico sale y asciende en silencio, sin llamas.
Eliminar...viaje interestelar aceleración constante (inteligencia artificial)... Dicen "creo que la humanidad no tiene ni idea de lo que hemos hecho"... que las Máquinas podrían llegar a tener Conciencia de Sí Mismas...y llegar a ser + Inteligentes que el ser humano...leerían los libros de Maquiavelo... si eso ocurre y el Robot de Compañía cree que Tu puedes ser un peligro para El... Peligro: xxx TERMINATOR xxx
ResponderEliminar(2)...viaje interestelar aceleración constante (sin tonterías relativistas: miles G)... ni las Masas ni la Gravedad ni las Órbitas de Marte y la Tierra son iguales. Por tanto las diferentes Aceleraciones que experimentan ambos planetas, gravitatorias y también en sus afelios y perihelios hacen que No "el Tiempo" sino "la Maquinaria" del reloj que mide su transcurso cambie. Aunque sea un reloj atómico, los electrones tienen masa y se ven afectados por esas aceleraciones cambiando no "el Tiempo" sino su medición. Ese Universo relativista no Infinito sino "curvo", con el cuento de que si vas en línea recta y pasas la curva "frontera" al otro lado hay "Nada". La Nada es lo único que no podemos ni siquiera imaginar, ¿sería esa "Nada" relativista tal vez un inmenso espacio relleno de turrón de Alicante? (del blando por favor). La velocidad no cambia el Tiempo, lo que cambia el ritmo de "la maquinaria" del reloj que lo mide son las fuerzas de Aceleración. Es el reloj el que atrasa o adelanta, no el Tiempo que realmente es el que dará o quitará razones.
ResponderEliminar...viaje interestelar constante aceleración (hipótesis tonyon)... "la velocidad orbital de los electrones varía inversamente a la aceleración", gravitatoria o de movimiento. Por eso en Marte con menor aceleración gravitatoria un reloj atómico va más rápido que en la Tierra. Es el reloj el que atrasa o adelanta, no "el Tiempo".
Eliminar(3a)...viaje interestelar constante aceleración (hipótesis tonyon)... con los futuros Transformadores Gravitatorios: qué pasaría si... Nave Estelar a 1 Millón G...Áreas habitables: ((igual que sumergidos en agua: aceleración constante hacia abajo↓ (gravedad) (-) el empuje constante (aceleración constante) desde el agua hacia arriba↑))... 1M-g de aceleración constante hacia el suelo ↓↓motores↓↓ (-) 999 999g de aceleración constante hacia el techo ↑↑transformadores gravitatorios↑ = 1g de aceleración constante hacia el suelo↓... Áreas habitables: 2 relojes atómicos fuera y 2 dentro. Los 2 dentro funcionan a 1g normalmente. Los 2 de fuera a 1M-g... quizás sus electrones se quedarían parados en sus órbitas: Los 2 relojes de fuera se pararían, no "el Tiempo" de fuera sí y el de dentro no. Si la atración electromagnética protón/electrón fuera más fuerte que las fuerzas de la enorme aceleración sobre los electrones, los electrones caerían al núcleo atómico quedando los átomos con sus electrones parados pegados al núcleo... Sin electrones de valencia ya no hay moleculas... Qué pasaría con la estructura de la Nave ("eso es la Materia, sobre todo espacio vacío") ya de Materia formada por átomos con los electrones parados en sus órbitas, o por átomos con sus electrones parados y pegados al núcleo: la estructura de la Nave se derrumbaría como arena sin cemento... Para evitar el "efecto aceleración" poner los Transformadores Gravitatorios en TODA la estructura de la Nave, no solo en las áreas habitables. Así la Nave entera siente 1g aunque vaya a 1M-g, (1Mega-g).
Eliminar...viaje interestelar constante aceleración (tonyon - Antonio Iglesias Noja - proyecto GSENA: Global Solar Energy No Accumulation)... del S☼L→ a la S☺mbra del giratorio Planeta envío recíproco Global de Electricidad por Cables Submarinos... Cubrir Desiertos con Paneles Solares en alto (bajo ellos el suelo mejora)... Sin "esos" malditos patriotas contra el Progreso de la Humanidad cortando los Cables.
ResponderEliminar(3a)...viaje interestelar aceleración constante (motor tonyon: Antonio Iglesias Noja)... Impulso a reacción con recuperación. Nada se Pierde. El "Río con Retorno". Nave Cuatrimotor, a Popa en "cola de flecha" las "toberas": 4 RECTÁNGULOS cada uno en forma de "Doble U"; todos los 2 lados menores en forma de ((Semicircunferencia)) para ampliar las Curvas; largos y estrechos iguales y opuestos, de *Tubos* al Vacío material No magnético de "x" medidas todos Alineados con el eje longitudinal de la Nave y rellenos a "½" de Imanes ◙◙ (doble largo que ancho para que no se giren dentro del *Tubo*) que van en Confinamiento Magnético a Repulsión MAGLEV, con sus Polos en Línea (o en transversal, si se usan imanes con sus polos en el doble ancho que largo) N-S con la Dirección de Avance, así: →|N◙◙S|↔|S◙◙N|↔|N◙◙S|↔|S◙◙N|→ "ajustados" dentro del *Tubo* pero con la holgura adecuada para ir sin roce ni atascarse "el Tren" en las Curvas... En línea con el eje longitudinal de la Nave: cada ◄═Ramal═Recto═de═Impulsión═→, un Cañón Electromagnético Gauss de alimentación continua (como una ametralladora) que Impulsa a gran velocidad a un Collar de pesados Imanes ◙◙ Sueltos: ◄1º Impulso a reacción→ ◙◙... Cada Imán del Collar, algo Separado de los demás, sale disparado del Cañón ◙◙→ luego sigue a inercia y tras la Curva )) va por el otro ◄═Ramal←◙◙↔◙◙↔◙◙↔◙◙═Recto═de═Retorno═← que tiene Bobinas Electromagnéticas para frenado parcial (aquí, ya más lentos, los Imanes se acumulan) donde ahora ya se le va Frenando ««« ◙◙ »» y por ello ◄Transfiere su Momento Lineal hacia Proa← como: ◄2º Impulso, para tras la Curva (( Entrar siempre a la misma velocidad más Lenta de nuevo al ◙◙→ Cañón indefinidamente: Recuperación. Nada se Pierde, "solo" hace falta mucha energía eléctrica en la Nave: un Generador Nuclear.
ResponderEliminar(3b)...viaje interestelar aceleración constante (motor tonyon: Antonio Iglesias Noja)... Impulso a reacción con recuperación. Nada se Pierde. "Los Ríos con Retorno". Nave Cuatrimotor funcionando normalmente en modo Bimotor con los 2 Opuestos (con 1 solo motor/rectángulo el "problema" con el proyectil al girar cada curva: adquiere Momento Angular; momento lineal x distancia al eje de giro; se origina un vector de fuerza a reacción lateral contraria que haría girar la Nave (como la hélice de cola de un helicóptero). Por ello con 2 Motores/Rectángulo Opuestos funcionando sincronizados al unísono sus proyectiles toman las Curvas en sentido contrario con Resultante en la Nave de fuerza nula de giro)... a Popa en "cola de flecha" las "toberas": 4 RECTÁNGULOS cada uno en forma de "Doble U"; todos los 2 lados menores en forma de ((Semicircunferencia)) para ampliar las Curvas; largos y estrechos iguales y opuestos, de *Tubos* al Vacío material No magnético de "x" medidas todos Alineados con el eje longitudinal de la Nave y rellenos: (Confinamiento Magnético: Bolas Acero imantadas, se giran y no pueden ir. Bolas Acero no imantadas, tendrían que ir en atracción alrededor)... a "½" de Imanes ◙◙ (doble largo que ancho para que no se giren dentro del *Tubo*) que van en Confinamiento Magnético a Repulsión MAGLEV, con sus Polos en Línea (o en transversal, si se usan imanes con sus polos en el doble ancho que largo) N-S con la Dirección de Avance, así: →|N◙◙S|↔|S◙◙N|↔|N◙◙S|↔|S◙◙N|→ "ajustados" dentro del *Tubo* pero con la holgura adecuada para ir sin roce ni atascarse "el Tren" en las Curvas... En línea con el eje longitudinal de la Nave: cada ◄═Ramal═Recto═de═Impulsión═→, un Cañón Electromagnético Gauss de alimentación continua (como una ametralladora) que Impulsa a gran velocidad a un Collar de pesados Imanes ◙◙ Sueltos: ◄1º Impulso a reacción→ ◙◙... Cada Imán del Collar, algo Separado de los demás, sale disparado del Cañón ◙◙→ luego sigue a inercia y tras la Curva )) va por el otro ◄═Ramal←◙◙↔◙◙↔◙◙↔◙◙═Recto═de═Retorno═← que tiene Bobinas Electromagnéticas para frenado parcial (aquí, ya más lentos, los Imanes se acumulan) donde ahora ya se le va Frenando ««« ◙◙ »» y por ello ◄Transfiere casi todo su Momento Lineal (masa x velocidad) hacia Proa← como: ◄2º Impulso, para tras la Curva (( Entrar siempre a la misma velocidad más Lenta de nuevo al ◙◙→ Cañón indefinidamente: Recuperación. Nada se Pierde, "solo" hace falta mucha energía eléctrica en la Nave: un Generador Nuclear.
ResponderEliminar...viaje interestelar aceleración constante (el Motor de "Impulso a reacción con recuperación")... Conclusión: a falta de prueba práctica, en teoría No Funciona, por la conservación del momento lineal: Al estar sujeto a la Nave el sistema Motor, el proyectil al girar 180º produce fuerza a reacción contraria anulando la fuerza a reacción de avance anterior: La Nave no se mueve. Como al activar la Reversa que desvía el empuje 180º y frena un avión reactor ya en el suelo al aterrizar. Fin.
Eliminar(1)...viaje interestelar aceleración constante (motor Iglesias)... Impulso a reacción con recuperación. Nada se Pierde. El "Río con Retorno". Nave Cuatrimotor, funcionando normalmente en modo Bimotor con los 2 Opuestos... Con 2 Motores/Rectángulo Opuestos funcionando Sincronizados al unísono (por pedir que no quede) sus Proyectiles toman las Curvas Cada Uno En Sentido Contrario Al Otro , con Resultante en la Nave de fuerza nula de giro (momentos angulares y lineales)... A Popa en "cola de flecha" las "toberas". Cada Motor: 1 Solo *Tubo* sección circular largo arrollado formando así 1 RECTÁNGULO-Longitudinal-Principal, Todos conectados por el *Tubo* único a sus otros Rectángulos-Transversales-Secundarios de "desvío" del Momento Lineal (masa x velocidad). El *Tubo* Recto═Cañón de Ida al final ENTRA girando formando a 90º "varios" Rectángulos-Transversales-Superpuestos-Secundarios y SALE *Tubo* Recto═Retorno de vuelta en el Principal. Rectángulos Todos en forma de "Doble U"; todos los 2 lados menores en forma de ((Semicircunferencia)) para ampliar las Curvas; largos y estrechos iguales y opuestos, de *Tubos* al Vacío material No magnético de "x" medidas todos los Principales Alineados (lados mayores) con el eje longitudinal de la Nave y rellenos: (Confinamiento Magnético: Bolas Acero imantadas, se giran se pegan y no pueden ir separadas. Bolas Acero no imantadas, exteriores electroimanes toroidales (donuts))... rellenos a "½" de Cilindro◙◙Imanes (doble largo que ancho para que no se giren dentro del *Tubo*) que van en Confinamiento Magnético a Repulsión MAGLEV, CON sus Polos en Línea N-S con la Dirección de Avance, así: →|N◙◙S|↔|S◙◙N|↔|N◙◙S|↔|S◙◙N|→ "ajustados" dentro del *Tubo* pero con la holgura adecuada para ir sin roce ni atascarse "el Tren" en las Curvas... El más cerca y en línea con el eje longitudinal de la Nave: cada ◄◄═Ramal═Recto═de═Impulsión═►, un Cañón Electromagnético Gauss de alimentación continua (como una ametralladora) que Impulsa a gran velocidad a un Collar de pesados Imanes ◙◙ Sueltos: ◄◄Impulso a reacción→ ◙◙... Cada Imás del Collar, algo Separado de los demás, en Cada Cañón salen disparados ◙◙→ a la vez (momento lineal "salvaje") luego ambos siguen a inercia y Entran cada uno en sus Rectángulos-Transversales-Superpuestos (momento lineal "domado") que tienen ═←◙◙↔◙◙↔◙◙↔◙◙═← Bobinas Electromagnéticas Exteriores, solo en los transversales lados mayores, para frenado parcial (aquí, ya más lentos, los Imanes se acumulan) donde ambos van siendo Frenados y por ello ↔Transfieren↔ Momento Lineal (los lados mayores transversales) en ◄►Perpendicular◄► hacia o desde la Estructura Lateral de la Nave. Salen de los Transversales ◙◙→ y vuelven (momento lineal "manso") cada uno por su Principal ←═Ramal═←◙◙═Recto═de═Retorno═► para al unísono Entrar ambos siempre a la misma velocidad más Lenta de nuevo a su ◙◙→ Cañón indefinidamente: Recuperación. Nada se Pierde... La suma de los momentos locales es igual en Ida "salvaje" que en Vuelta "manso", pero en Ida Ramal═Cañón (fuerza reacción a favor) el momento lineal es mayor que en Vuelta Ramal═Retorno (recuperación: fuerza reacción en contra): La Nave avanza veloz... capturando del Espacio átomos de H y O para formar H2O: Agua! de beber y para... "solo" hace falta mucha energía eléctrica desde el Reactor de Fusión Nuclear, S☼L Artificial de la Nave Estelar.
ResponderEliminar(El Imán Más Fuerte del Mundo. Veritasium. YouTube). Levitación por la Ley de Lenz: corrientes inducidas en materiales no magnéticos sí conductores como Al, Cu. Todos los materiales tienen propiedades magnéticas: el agua es diamagnética: levitación de frutas y seres vivos.
ResponderEliminar